Utente:Grasso Luigi/sandbox4/Teoremi di isomorfismo

In matematica ci sono vari teoremi di isomorfismo, che asseriscono generalmente che alcuni insiemi dotati di opportune strutture algebriche sono isomorfe.

Teoria dei gruppi

In teoria dei gruppi ci sono tre teoremi d'isomorfismo, che valgono anche, con opportune modifiche, per anelli e moduli. I teoremi furono formulati originariamente da Richard Dedekind; successivamente Emmy Noether li rese più generali nell'articolo Abstrakter Aufbau der Idealtheorie in algebraischen Zahl und Funktionenkörpern pubblicato nel 1927 in Mathematische Annalen, per essere poi sviluppati nella forma moderna da Bartel Leendert van der Waerden nel suo libro Algebra.

Primo teorema d'isomorfismo

Se $f:G\to H$ è un omomorfismo fra due gruppi $G$ e $H$, allora il nucleo di $f$ è un sottogruppo normale di $G$, ed il gruppo quoziente $G/\operatorname {Ker} (f)$ è isomorfo all'immagine di $f$. In simboli:

$\operatorname {Ker} (f)\triangleleft G,\quad G/\operatorname {Ker} (f)\cong \operatorname {Im} (f)$

L'isomorfismo è canonico, indotto dalla mappa $f$: la classe $g\cdot \operatorname {Ker} (f)$ è mandata in $f(g)$.

Questo teorema è detto teorema fondamentale di omomorfismo.

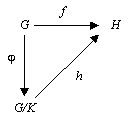
Proprietà universale del conucleo $G/K$

Se $f:G\to H$ è un omomorfismo e $K$ è un sottogruppo normale di $G$ contenuto in $ker(f)$, esiste un unico omomorfismo $h:G/K\to H$ tale che

$f=h\circ \varphi$

dove $\varphi$ è la proiezione canonica $G\to G/K$.

Secondo teorema d'isomorfismo (teorema del diamante)

Siano $H$ e $N$ due sottogruppi di un gruppo $G$, con $N$ sottogruppo normale. Allora il sottoinsieme prodotto

$HN=\{hn\,|\,h\in H,n\in N\}$

è anch'esso un sottogruppo di $G$, e inoltre:

• $N$ è normale anche in $HN$,
• $H\cap N$ è normale in $H$,
• $H/(H\cap N)\cong HN/N.$

L'isomorfismo è canonico, indotto dalla mappa

$H\to HN/N,\quad h\mapsto hN.$

Terzo teorema d'isomorfismo

Siano $H,N$ due sottogruppi normali di $G$ con $N$ contenuto in $H$. Vale il seguente isomorfismo:

$(G/N)/(H/N)\cong G/H.$

Anche questo isomorfismo è canonico.

Groups

We first present the isomorphism theorems of the groups.

Note on numbers and names

Below we present four theorems, labelled A, B, C and D. They are often numbered as "First isomorphism theorem", "Second..." and so on; however, there is no universal agreement on the numbering. Here we give some examples of the group isomorphism theorems in the literature. Notice that these theorems have analogs for rings and modules.

Comparison of the names of the group isomorphism theorems

Comment	Author	Theorem A	Theorem B	Theorem C
No "third" theorem	Jacobson	Fundamental theorem of homomorphisms	(Second isomorphism theorem)	"often called the first isomorphism theorem"
	van der Waerden, DurbinTemplate:Refn	Fundamental theorem of homomorphisms	First isomorphism theorem	Second isomorphism theorem
	Knapp	(No name)	Second isomorphism theorem	First isomorphism theorem
	Grillet	Homomorphism theorem	Second isomorphism theorem	First isomorphism theorem
Three numbered theorems	(Other convention per Grillet)	First isomorphism theorem	Third isomorphism theorem	Second isomorphism theorem
	Rotman	First isomorphism theorem	Second isomorphism theorem	Third isomorphism theorem
	Fraleigh	Fundamental homomorphism theorem or first isomorphism theorem	Second isomorphism theorem	Third isomorphism theorem
	Dummit & Foote	First isomorphism theorem	Second or Diamond isomorphism theorem	Third isomorphism theorem
No numbering	Milne	Homomorphism theorem	Isomorphism theorem	Correspondence theorem
	Scott	Homomorphism theorem	Isomorphism theorem	Freshman theorem

It is less common to include the Theorem D, usually known as the lattice theorem or the correspondence theorem, as one of isomorphism theorems, but when included, it is the last one.

Statement of the theorems

Theorem A (groups)

Diagram of the fundamental theorem on homomorphisms

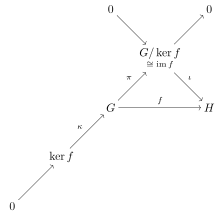
Let G and H be groups, and let f : G → H be a homomorphism. Then:

1. The kernel of f is a normal subgroup of G,
2. The image of f is a subgroup of H, and
3. The image of f is isomorphic to the quotient group G / ker(f).

In particular, if f is surjective then H is isomorphic to G / ker(f).

This theorem is usually called the first isomorphism theorem.

Theorem B (groups)

Diagram for theorem B4. The two quotient groups (dotted) are isomorphic.

Let $G$ be a group. Let $S$ be a subgroup of $G$, and let $N$ be a normal subgroup of $G$. Then the following hold:

1. The product $SN$ is a subgroup of $G$,
2. The subgroup $N$ is a normal subgroup of $SN$,
3. The intersection $S\cap N$ is a normal subgroup of $S$, and
4. The quotient groups $(SN)/N$ and $S/(S\cap N)$ are isomorphic.

Technically, it is not necessary for $N$ to be a normal subgroup, as long as $S$ is a subgroup of the normalizer of $N$ in $G$. In this case, $N$ is not a normal subgroup of $G$, but $N$ is still a normal subgroup of the product $SN$.

This theorem is sometimes called the second isomorphism theorem, diamond theorem or the parallelogram theorem.

An application of the second isomorphism theorem identifies projective linear groups: for example, the group on the complex projective line starts with setting $G=\operatorname {GL} _{2}(\mathbb {C} )$, the group of invertible 2 × 2 complex matrices, $S=\operatorname {SL} _{2}(\mathbb {C} )$, the subgroup of determinant 1 matrices, and $N$ the normal subgroup of scalar matrices $\mathbb {C} ^{\times }\!I=\left\{\left({\begin{smallmatrix}a&0\\0&a\end{smallmatrix}}\right):a\in \mathbb {C} ^{\times }\right\}$, we have $S\cap N=\{\pm I\}$, where $I$ is the identity matrix, and $SN=\operatorname {GL} _{2}(\mathbb {C} )$. Then the second isomorphism theorem states that:

$\operatorname {PGL} _{2}(\mathbb {C} ):=\operatorname {GL} _{2}\left(\mathbb {C} )/(\mathbb {C} ^{\times }\!I\right)\cong \operatorname {SL} _{2}(\mathbb {C} )/\{\pm I\}=:\operatorname {PSL} _{2}(\mathbb {C} )$

Theorem C (groups)

Let $G$ be a group, and $N$ a normal subgroup of $G$. Then

1. If $K$ is a subgroup of $G$ such that $N\subseteq K\subseteq G$, then $G/N$ has a subgroup isomorphic to $K/N$.
2. Every subgroup of $G/N$ is of the form $K/N$ for some subgroup $K$ of $G$ such that $N\subseteq K\subseteq G$.
3. If $K$ is a normal subgroup of $G$ such that $N\subseteq K\subseteq G$, then $G/N$ has a normal subgroup isomorphic to $K/N$.
4. Every normal subgroup of $G/N$ is of the form $K/N$ for some normal subgroup $K$ of $G$ such that $N\subseteq K\subseteq G$.
5. If $K$ is a normal subgroup of $G$ such that $N\subseteq K\subseteq G$, then the quotient group $(G/N)/(K/N)$ is isomorphic to $G/K$.

The last statement is sometimes referred to as the third isomorphism theorem. The first four statements are often subsumed under Theorem D below, and referred to as the lattice theorem, correspondence theorem, or fourth isomorphism theorem.

Theorem D (groups)

Let $G$ be a group, and $N$ a normal subgroup of $G$. The canonical projection homomorphism $G\rightarrow G/N$ defines a bijective correspondence between the set of subgroups of $G$ containing $N$ and the set of (all) subgroups of $G/N$. Under this correspondence normal subgroups correspond to normal subgroups.

This theorem is sometimes called the correspondence theorem, the lattice theorem, and the fourth isomorphism theorem.

The Zassenhaus lemma (also known as the butterfly lemma) is sometimes called the fourth isomorphism theorem.

Discussion

The first isomorphism theorem can be expressed in category theoretical language by saying that the category of groups is (normal epi, mono)-factorizable; in other words, the normal epimorphisms and the monomorphisms form a factorization system for the category. This is captured in the commutative diagram in the margin, which shows the objects and morphisms whose existence can be deduced from the morphism $f:G\rightarrow H$. The diagram shows that every morphism in the category of groups has a kernel in the category theoretical sense; the arbitrary morphism f factors into $\iota \circ \pi$, where ι is a monomorphism and π is an epimorphism (in a conormal category, all epimorphisms are normal). This is represented in the diagram by an object $\ker f$ and a monomorphism $\kappa :\ker f\rightarrow G$ (kernels are always monomorphisms), which complete the short exact sequence running from the lower left to the upper right of the diagram. The use of the exact sequence convention saves us from having to draw the zero morphisms from $\ker f$ to $H$ and $G/\ker f$.

If the sequence is right split (i.e., there is a morphism σ that maps $G/\operatorname {ker} f$ to a Template:Pi-preimage of itself), then G is the semidirect product of the normal subgroup $\operatorname {im} \kappa$ and the subgroup $\operatorname {im} \sigma$. If it is left split (i.e., there exists some $\rho :G\rightarrow \operatorname {ker} f$ such that $\rho \circ \kappa =\operatorname {id} _{{\text{ker}}f}$), then it must also be right split, and $\operatorname {im} \kappa \times \operatorname {im} \sigma$ is a direct product decomposition of G. In general, the existence of a right split does not imply the existence of a left split; but in an abelian category (such as that of abelian groups), left splits and right splits are equivalent by the splitting lemma, and a right split is sufficient to produce a direct sum decomposition $\operatorname {im} \kappa \oplus \operatorname {im} \sigma$. In an abelian category, all monomorphisms are also normal, and the diagram may be extended by a second short exact sequence $0\rightarrow G/\operatorname {ker} f\rightarrow H\rightarrow \operatorname {coker} f\rightarrow 0$.

In the second isomorphism theorem, the product SN is the join of S and N in the lattice of subgroups of G, while the intersection S ∩ N is the meet.

The third isomorphism theorem is generalized by the nine lemma to abelian categories and more general maps between objects.

Teoria degli anelli

The statements of the theorems for rings are similar, with the notion of a normal subgroup replaced by the notion of an ideal.

Theorem A (rings)

Let $R$ and $S$ be rings, and let $\varphi :R\rightarrow S$ be a ring homomorphism. Then:

1. The kernel of $\varphi$ is an ideal of $R$,
2. The image of $\varphi$ is a subring of $S$, and
3. The image of $\varphi$ is isomorphic to the quotient ring $R/\ker \varphi$.

In particular, if $\varphi$ is surjective then $S$ is isomorphic to $R/\ker \varphi$.

Theorem B (rings)

Let R be a ring. Let S be a subring of R, and let I be an ideal of R. Then:

1. The sum S + I = {s + i | s ∈ S, i ∈ I } is a subring of R,
2. The intersection S ∩ I is an ideal of S, and
3. The quotient rings (S + I) / I and S / (S ∩ I) are isomorphic.

Theorem C (rings)

Let R be a ring, and I an ideal of R. Then

1. If $A$ is a subring of $R$ such that $I\subseteq A\subseteq R$, then $A/I$ is a subring of $R/I$.
2. Every subring of $R/I$ is of the form $A/I$ for some subring $A$ of $R$ such that $I\subseteq A\subseteq R$.
3. If $J$ is an ideal of $R$ such that $I\subseteq J\subseteq R$, then $J/I$ is an ideal of $R/I$.
4. Every ideal of $R/I$ is of the form $J/I$ for some ideal $J$ of $R$ such that $I\subseteq J\subseteq R$.
5. If $J$ is an ideal of $R$ such that $I\subseteq J\subseteq R$, then the quotient ring $(R/I)/(J/I)$ is isomorphic to $R/J$.

Theorem D (rings)

Let $I$ be an ideal of $R$. The correspondence $A\leftrightarrow A/I$ is an inclusion-preserving bijection between the set of subrings $A$ of $R$ that contain $I$ and the set of subrings of $R/I$. Furthermore, $A$ (a subring containing $I$) is an ideal of $R$ if and only if $A/I$ is an ideal of $R/I$.

Teoria dei numeri

In teoria dei numeri, esiste il seguente teorema d'isomorfismo di Ax-Kochen. Il teorema afferma che se $(A,S,z)$ e $(A',S',z')$ sono terne di Peano allora esiste una mappa $\varphi \colon A\to A'$ tale che:

• $\varphi$ è biiettiva;
• $\varphi (z)=z'$;
• $\varphi (S(a))=S'(\varphi (a))$.